SegReg :   calculator for segmented (piecewise) linear regression (in splines) with breakpoint
Totally free download of software

Summary:
The SegReg computer program (model) is designed to perform a segmented (piecewise) linear regression (in splines) of one dependent (response) variable )Y, e.g. plant growth, crop yield) on one (X) or two (X and Z) independent (explanatory, causal, ifluential) variables (predictors), e.g. crop growth factors like depth of water table and soil salinity. It can also be condidered as a regression calculator.
Details:
The segmentation is done by introducing a breakpoint (break-point, threshold, switching point). Thus one can obtain a broken, discontinuous, line. Seven types of functions (0 to 6) are used. Examples are given below.
      The selection of the best function type and breakpoint is based on maximizing the statistical coefficient of explanation (determination) and performing the test of significance.
      The 90% confidence interval (belt) is given as well as an Anova table for variance analysis.
In December 2008, an amplified version of the SegReg calculator (SegRegA) was made permitting the use of weight factors, preferred regression type or type exclusion. Although it can lead to manipulation, it is available on request.
      More details are found in the program itself.

Start:
The mathematical model starts clicking on SegReg.Exe.

Documentation:

A paper on the statistical principles of segmented regression with break-point, including the determination of its confidence interval, can be inspected in here.
      The construction of confidence intervals of the regression segments separated by the breakpoint, and of the breakpoint itself, is described in this confidence paper, which also gives an example. The calculation of standard error of the breakpoint can be found in the BP paper. The intervals are made with Student's t-distribution, see the t-test program.
      The principles of regression analysis in general can be found in this lecture note.
Furter, the analysis of variance (Anova) and the F-test for segmented linear regression with break-point, as used in the SegReg model calculator, is briefly discussed in this paper.
A lecture note on statistical analysis with examples of SegReg program applications is found in a document called Data Analysis.
      A lecture note providing an overview of segmented regression types as well as a summary of statistical criteria for finding the best fitting type as well as the optimal value of the breakpoint is to be read at regression types
      A paper on the use of SegRegA for the fitting of S-curves to functions with a dependent variable (Y) and an influential variable (X) can be found as a pdf document
      See here a list of articles and publications using the SegReg calculator app.


Acknowledgements
In September 2010, the SegReg program calculator was provided with new functionalities thanks to a request by Kirsten Otis so that the model permits extra applications.
      In March 2011 the confidence belts were improved thanks to questions raised by Linda Jung.
In October 2012 the confidence block of the breakpoint for type 2 functions was improved thanks to questions raised by John Schukman.
      In March 2013 the use of a second independent variable was updated thanks to comments made by Barbara Mahler.
In November 2013 the calculation of the standard error and confidence interval of the breakpoint (BP), as well as of the Y value at BP, was standardized for the different types of segmented regression. A description of the mathematics involved, with examples, can be seen in this confidence paper. These changes were motivated by suggestions put forward by Dawn Noren and Wenhuai Li.
      In January 2014 the conditions for Type 2, 3, 4 and 5 were made more strict thanks to an example provided by John Shukman.
Experiences: For improvement, I am interested to learn about your experiences with SegReg. For this, there is a contact form.

Download:
SegReg
standard

Download:
SegRegA
amplified

Go to:

Software
& models

General articles
& manuals

Artículos
(in Spanish,
 en Español)

Published
reports & cases

Particular
reports & cases

FAQ's
& answers

Home
page

Alternatives

(1) - An amplification application of the SegReg calculator permitting expression of preference for a certain type of segmentation, or of the wish to exclude a certain type, can be downloaded from SegRegA. It also gives the option to select an S-curve, power function, or a generalized third degree polynoom, see: S-curves, Cubic, Power or, Polynome.
(2) - A different version of SegReg, called PartReg has been developed with the aim to detect the largest possible horizontal stretch (plateau) in Type 3 and Type 4 relations. This has been done to find the maximum tolerance (plateau or "no effect" reach) of the dependent variable - e.g. crop yield - for changes in the dependent variable (e.g. soil salinity or depth of the water table).
      Download PartReg with this link See the figures below to appreciate the difference between SegReg and PartReg. The first minimizes the deviations of the model values from the observed ones over the entire domain, whereas the second calculates the maximum part (range) of the domain over which the regression coefficient (i.e. the slope of the regression line) can be taken equal to zero.

See also

For more examples see this segmented regression article on page 13 and following, the tolerance paper on soil salinity tolerance of crops, or the sensitivity paper on sensitivity of crops to shallow watertables.
      Segreg permits the analysis of one dependent and two independent variables. This case is called polynomial. See the screen print of the input menu for such a case in Part 2 of the illustrations below. Some results are also shown there.
      Relations of crop yield and depth of water table: crop-watertable .
Yearly average day temperatures in the Netherlands and global warming: average temperatures .
Yearly maximum day temperatures in the Netherlands and global warming: maximum temperatures .
Segmented and probability analysis: segments and probability.
Comparing the regressions of Y-X data by means of the amplified power function using Solver in Excel and SegRegA with graphics.
Testing the statistical significance of the improvement of cubic regression compared to quadratic regression using analysis of variance (ANOVA): testing.



Part 1 of the illustrations for 1 dependent and one variable (Y and X respectively).
(Part 2 for the polynomal case of 1 dependent variable (Y) and 2 independent variables (X and Z) can be seen further down)
Introduction screen of SegReg calculator program:
introdcution to segreg
The model comes with various explanations like programmed function types, calculation methods, and application of significance tests.

  Example Type 3:
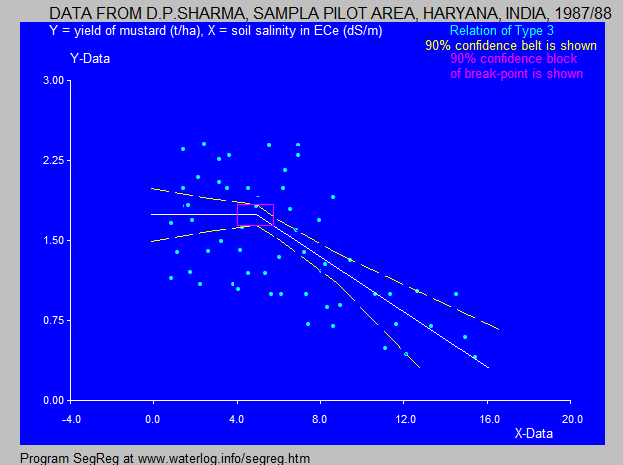
yield of mustard versus soil salinity
The SegReg model is designed for segmented (piecewise) linear regression with breakpoint (threshold). The application program can be used for salt tolerance of crops or the tolerance to shallow watertables.
The calculator clarifies the crop response and demonstrates the resistance to high soil salinity or water level. This Type 3 is similar to the Maas-Hoffman model having a plateau.

Example Type 3 with extended horizontal line (plateau) using the same data as above in the PartReg software application instead of SegReg.
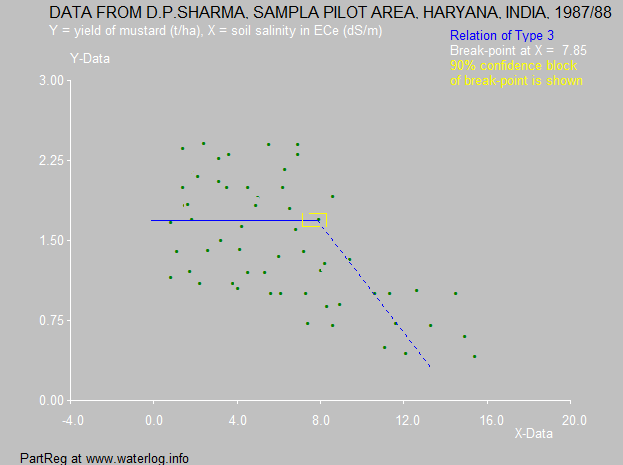
Mustard and salinity with partial regression
According to this calculator model, the salt tolerance of mustard is almost ECe=8 dS/m. After this threshold (breakpoint, knot)the yield reduces. In other words, from this application program it can be deduced that the crop resists salinity up to 8 dS/m while up to 8 dS/m there is no negative effect.

Example Type 4:
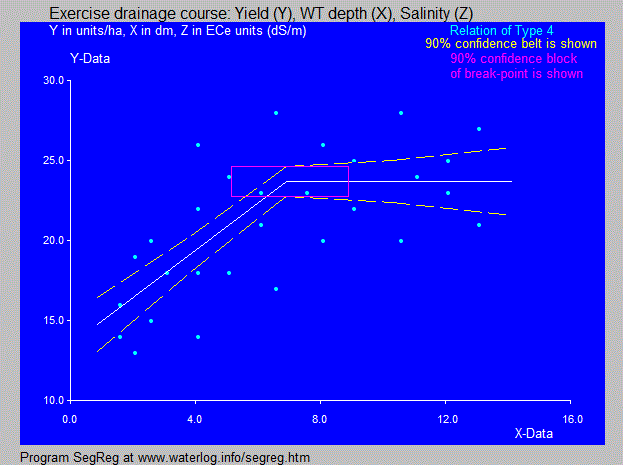
 example segreg type 4

The crop tolerates a depth of the water table of 7 dm.
The Segreg software calculator is an application (app) made to detect different segmented models, like Type 4 with a plateau in the above figure.
This type is an inverted Type 3 or an inverted Maas-Hoffman model. The breakpoint is also called knot.

  Example Type 5:
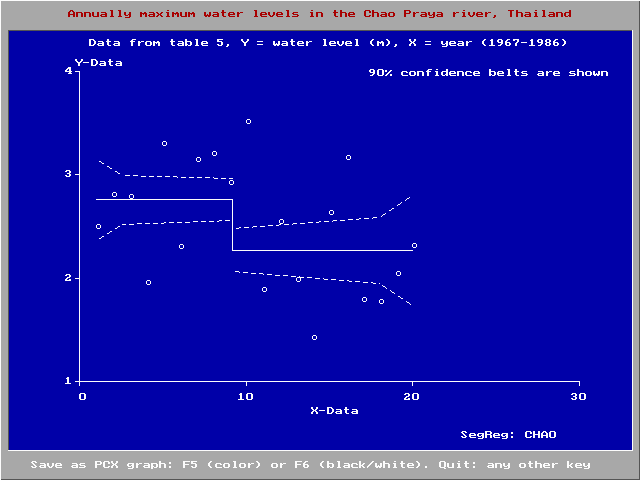
 segmented regression type 5

In year 9 (1976) a dam was contstructed in the river
The Segreg application (app) is a calculator made to program different segmented models, for example Type 5 in the figure.


Part 2 for the polynomal case of 1 dependent variable (Y) and 2 independent variables (X and Z)

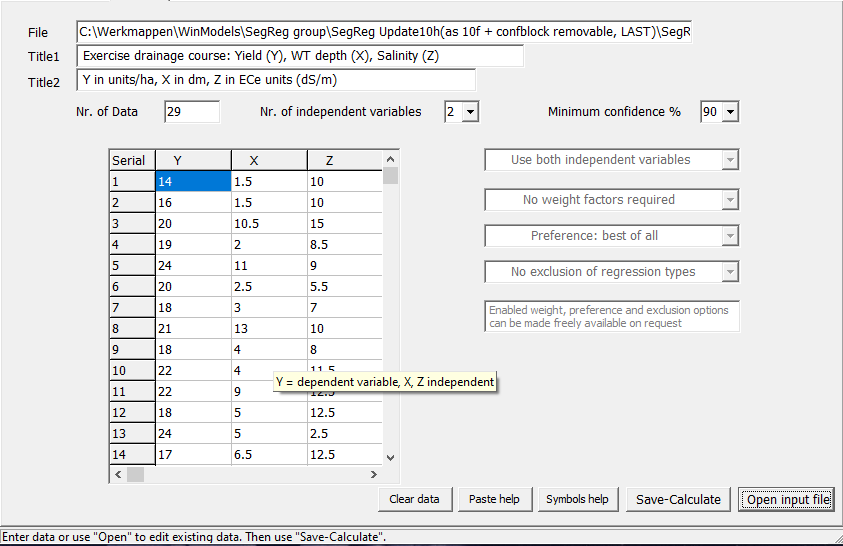
screen print polynomial

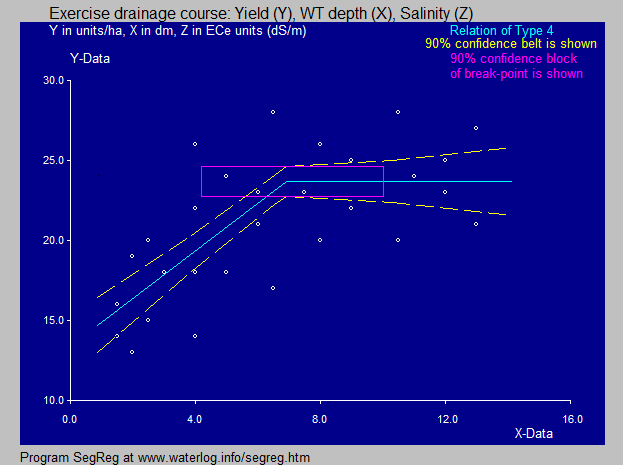
Screen print of the input menu for the polynomial case (1 dependent variable (Y) and 2 independent variables (X and Z). first independent variable
The SegReg program found that the 1st independent variable (X) has a higher coefficient of explanation than the second (Z). Therefore the first segemented regression is made for X.

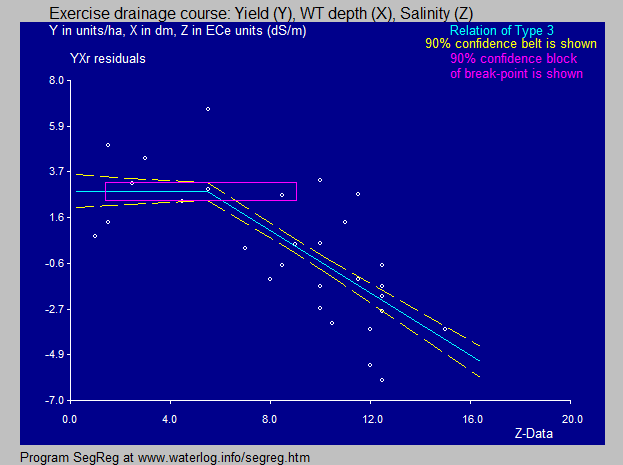
second independent variable
The the residuals of Y after the regression on X are used with a segmented regression on the second variable (Z).
The mathematical combination of the first and second analysis yields equations of the type Y = A.X + B.Z + C (polynomial)